Cocke-Younger-Kasami-Algorithmus - Theorie und Beispiel
Der Cocke-Younger-Kasami-Algorithmus, kurz CYK-Algorithmus, ist eine Bottom-up-Parsing-Technik für Grammatiken in Chomsky-Normalform.
Dieser Algorithmus kann verwendet werden, um zu prüfen, ob ein Wort durch eine kontextfreie Grammatik erzeugt werden kann.
Für die kontextfreie Grammatik (CFG) gilt Folgendes:
G = (V, Σ, P, S), wobei
V ist eine endliche Menge von Variablen (alternativ Nichtterminale, Nichtterminalsymbole)
Σ (mit V ∩ Σ= ∅) ist ein Alphabet von Zeichen (alternativ Terminale, Terminalsymbole)
P ist eine endliche Menge von Produktionen von der Form l -> r,
wobei l ∈ (V ∩ Σ= ∅)+ und r ∈ (V ∩ Σ= ∅)*
S ∈ V ist das Startsymbol (alternativ Startvariable)
Die folgende Regel gilt für die Chomsky-Normalform (CNF) mit der Grammatik G = (V, Σ, P, S):
A -> BC
A -> a
Eine CFG G = (V, Σ, P, S) mit ε ∉ L(G) ist in Chomsky-Normalform,
wenn für jede Produktion A -> w ∈ P gilt: w = a ∈ Σ oder w = BC mit B, C ∈ V.
a ist ein Terminalsymbol und A,B und C sind Nichtterminale.
Es gibt zwei verschiedene Verfahren zum Rechnen mit dem CYK-Algorithmus: Den CYK-Algorithmus von Endrullis und den Standard-CYK-Algorithmus.
Werfen wir zunächst einen Blick auf den CYK-Algorithmus von Endrullis.
Sei w = abbb und G = ({S, A,B}, {a, b}, P, S) mit P = {S → AB, A → BB | a, B -> AB | b}

(Quelle: http://joerg.endrullis.de/automata/12_parsing_cyk.pdf/print_12_parsing_cyk.pdf, Seite 4)
Erklärung: Zuerst schauen wir uns an, wie viele verschiedene Teilwörter in dem Wort "abbb" vorkommen. In dem Fall haben wir "a" und "b" und beide Teilwörter sind in der Grammatik definiert.
Als nächstes teilen wir das Wort "abbb" in 2er-Paare: "ab" und "bb". Wir überprüfen, ob das Ergebnis in der Grammatik definiert ist. Für "AB" haben wir "S, B" und für "BB" haben wir "A".
Danach nehmen wir die ersten drei Buchstaben ("abb") und die letzten drei Buchstaben ("bbb").
Für "abb" haben wir zwei mögliche Kombinationen, die wir berechnen können: "a" und "bb" , sowie "ab" und "b". Da wir schon im vorherigen Schritt berechnet haben, können wir einfach die Wörter kombinieren: "a" und "bb" ergibt "AA" und "ab" und "b" haben wir "SB, BB". Wir haben dann "BB", die in der Grammatik definiert wurde (A -> BB).
Bei "bbb" wird ebenfalls genauso berechnet wie "abb"
Zum Schluss haben wir das Wort "abbb". Da haben wir drei verschiedene Kombinationsmöglichkeiten: "a" und "bbb", "ab" und "bb", "abb" und "b".
Für "a" und "bbb": "AS, AB"
Für "ab" und "bb": "SA, BA"
Für "abb" und "b": "AB"
Da "AB" in der Grammatik schon definiert ist (S und B) sind wir mit der Berechnung fertig, weil zum Schluss ein "S" steht.
Zur Überprüfung könnt ihr mal ableiten, um zu schauen, ob ihr bei der Berechnung mit dem neuen CYK-Algorithmus einen Fehler gemacht habt (siehe letzte Zeile im Bild 1).
Der CYK-Algorithmus von Endrullis ist nicht der Standardalgorithmus. Der Unterschied zwischen den beiden besteht in der Darstellung und dem Berechnungsweg beim CYK-Algorithmus.
Beim CYK-Algorithmus von Endrullis wird das Wort in Teilwörter zerlegt und diese werden dann in aufsteigenden Wortpaaren berechnet. Zuerst wird ein Teilwort berechnet, dann in Paaren von 2 usw.
Beim Standard-CYK-Algorithmus wird die Berechnung anhand einer V(i,j)-Tabelle durchgeführt. Nehmen wir das gleiche Beispiel von oben.
Zuerst schreibt man das Wort auf. Danach zählt man, wie viele Buchstaben das Wort hat (in diesem Fall sind es 4, also kann man eine Tabelle mit i = j = 4 erstellen)
Überprüfen wir dann, ob "a" und "b" in der Grammatik definiert wurden. Also trägt man folgendes V(i,1)-Einträge in die Tabelle ein:
V(1,1)= A
V(2,1) = B
V(3,1) = B
V(4,1) = B
Als nächstes sehen wir uns die zweite Zeile an. Hier muss man darauf achten, dass die nächsten Schritte mit der 3-fach-Schleife berechnet werden:
V(1,2): j=2, i=1, k=1: V(1,2) = V(1,2) ∪ {A | A -> BC, B ∈ V(1,1), C ∈ V(2,1)}
V(2,2): j=2, i=2, k=1: V(2,2) = V(2,2) ∪ {A | A -> BC, B ∈ V(2,1), C ∈ V(3,1)}
V(3,2): j=2, i=3, k=1: V(3,2) = V(3,2) ∪ {A | A -> BC, B ∈ V(3,1), C ∈ V(4,1)}
Erläuterung: Für V(1,2) prüfen wir, ob das Teilwort „AB“, das aus V(1,1) und V(2,1) zusammengesetzt ist, in der Grammatik definiert ist. Da „AB“ sowohl in „S“ als auch in „B“ vorkommt, schreiben wir S,B für V(2,1). Und für V(2,2), im Beispiel auch V(3,2), betrachten wir das Teilwort „BB“. In der Grammatik ist „A -> BB“ definiert, also schreiben wir „A“ für V(2,2) und für V(3,2).
Dann schauen wir uns die dritte Zeile an. Sie haben sich vielleicht gefragt, warum in der vorherigen Berechnung k verwendet wurde. Der Grund ist, dass es verschiedene Möglichkeiten gibt, das Teilwort zu bestimmen, je weiter man Zeile für Zeile rechnet:
V(1,3): j=3, i=1, k=1: V(1,3) = V(1,3) ∪ {A | A -> BC, B ∈ V(1,1), C ∈ V(2,2)}
V(1,3): j=3, i=1, k=2: V(1,3) = V(1,3) ∪ {A | A -> BC, B ∈ V(1,2), C ∈ V(3,1)}
V(2,3): j=3, i=2, k=1: V(2,3) = V(2,3) ∪ {A | A -> BC, B ∈ V(2,1), C ∈ V(3,2)}
V(2,3): j=3, i=2, k=2: V(2,3) = V(2,3) ∪ {A | A -> BC, B ∈ V(2,2), C ∈ V(4,1)}
Erläuterung: In der dritten Zeile ist zu beachten, dass es zwei mögliche Teilwörter für V(1,3) und V(2,3) gibt, die in der Grammatik definiert sind.
In V(1,3) haben wir zwei Teilwörter: „AA“ (aus V(1,1) und V(2,2)) und ‚SB, BB‘ (aus V(1,2) und V(3,1)). „AA“ und ‚SB‘ sind in der Grammatik nicht definiert. Stattdessen haben wir das Teilwort „BB“, das in der Grammatik als „A“ markiert ist.
Und in V(2,3) haben wir auch zwei Teilwörter: „BA“ (aus V(2,1) und V(3,2)) und ‚AB‘ (aus V(2,2) und V(4,1)). BA“ ist nicht in der Grammatik enthalten, aber für ‚AB‘ haben wir ‚S‘ und ‚B‘.
Betrachten wir schließlich die letzte Zeile. Hier gibt es drei verschiedene Unterwörter, die in der Grammatik enthalten sind:
V(1,4): j=4, i=1, k=1: V(1,4) = V(1,4) ∪ {A | A -> BC, B ∈ V(1,1), C ∈ V(2,3)}
V(1,4): j=4, i=1, k=2: V(1,4) = V(1,4) ∪ {A | A -> BC, B ∈ V(1,2), C ∈ V(3,2)}
V(1,4): j=4, i=1, k=3: V(1,4) = V(1,4) ∪ {A | A -> BC, B ∈ V(1,3), C ∈ V(4,1)}
Erläuterung: Wie bereits erwähnt, haben wir hier drei verschiedene Teilwörter: „AS, AB“ (aus V(1,1) und V(2,3)), ‚SA, BA‘ (aus V(1,2) und V(3,2)) und ‚AB‘ (aus V(1,3) und V(4,1)).
Wir prüfen, ob wir die Teilwörter in der Grammatik gefunden haben. Und das ist nur bei „AB“ der Fall. Also schreiben wir „S,B“ für V(1,4).
Damit ist die Berechnung abgeschlossen. Nun prüfen wir, ob das Wort „abbb“ in der Sprache vorkommt. Wichtig ist, dass „S“ am Ende steht, im Beispiel bei V(1,4), was hier der Fall ist.
Wir können also die Antwort schreiben:
Da S ∪ V(1,4) gilt w ∪ L(G).
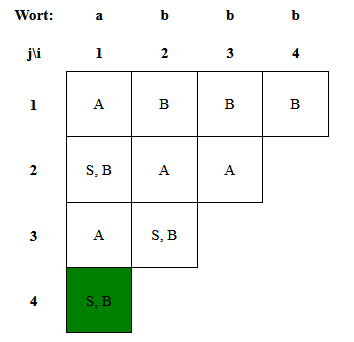
Wie wir sehen können, hat der Standard-CYK-Algorithmus eine einfache und klare Darstellung.
Das Problem ist, dass die Berechnung längerer Wörter sehr zeitaufwändig ist.
Daher ist der CYK-Algorithmus eine Alternative, da das Endergebnis in nur wenigen Schritten erzielt werden kann.